点击数:11090
翻译自Jay Alammar的一篇文章。 Translated from an article by Jay Alammar
原文地址: https://jalammar.github.io/visual-numpy/
有兴趣的还可以来看看Neo4j导入思知开源的1.4亿规模的中文知识图谱
正文开始:

NumPy 包是Python生态中数据分析,机器学习和科学计算领域的主力工具包。它极大地简化了对向量和矩阵地处理。一些主要的开发工具包也是基于 NumPy 作为基础工具包来开发的,比如 scikit-learn, SciPy, pandas, and tensorflow 。除了对数值数据进行切片和交叉分析,掌握Numpy为在你处理和调试这些库的时候给你带来优势。
在这篇文章中,在我们应用到机器学习模型之前,我们会看到 NumPy 的主要使用方式以及它如何展示不同类型的数据(表格,图像,文本等)
import numpy as np
创建数组
我们可以通过传递一个 python 列表,使用方法 “np.array()” 创建一个 NumPy 数组。如下图,python创建了一个如右图所示的数组:
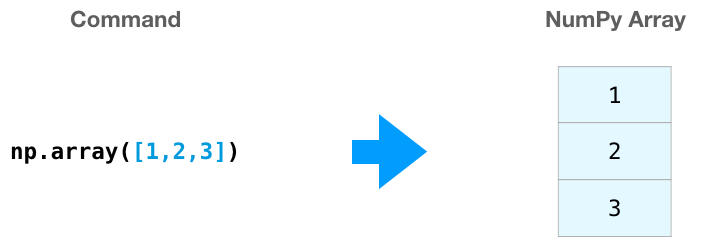
在很多场景下,我们希望 NumPy 能够帮我们初始化数组。 NumPy 提供了一些方法,比如 ones(), zeros() 和 random.random()。 我们只需要提供数组大小,如图:
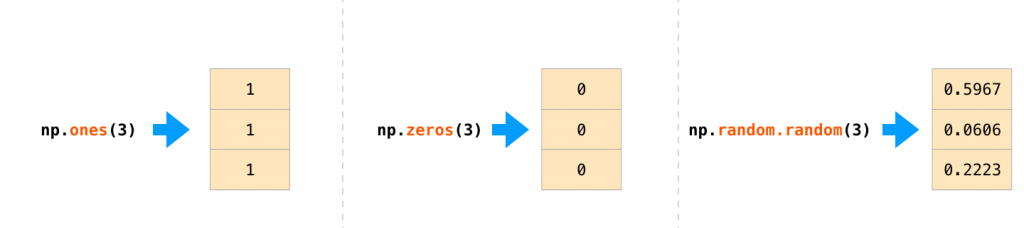
一旦创建好数组后,就可以自由地操纵他们了。
数组运算
我们首先创建两个 NumPy 数组,一个是 data 数组,一个是 ones数组:

将他们按照位置顺序(比如每行的值)相加,data + ones:
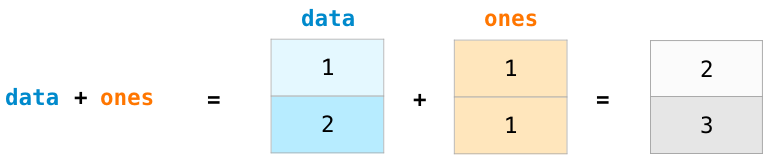
当我学这些的时候我意识到这可以让我不需要在代码中使用循环来计算这些。这种抽象能让你站在更高的角度去考虑问题。并且,不只有加法,我们还可以以如下方式去计算:

有一些经常需要计算一个数组和一个数字的操作(也称作对向量和标量的操作)。比如,我们的数组用英里表示距离,我们想转换成公里( 1英里(mi) = 1.60934千米(公里) ),可以使用:data * 1.6:

可以看到 NumPy 的乘法机制是对每一个单元都进行计算,这是称作 广播(broadcast)的一种机制,是非常有用的。
索引
我们可以对 NumPy 数组进行索引或者切片就像对 python 列表一样的操作:

聚合
NumPy 提供的另外一个优点是聚合功能:

除了 min, max 和 sum, 还有 mean 可以获取平均值,prod 可以获取所有元素相乘的结果, std 可以获取标准差,等等其他功能
多维
目前我们看到的例子都是一维向量。 NumPy 一个优雅的特性就是能将我们目前看到的所有特性扩展到任何维度。
创建矩阵
我们可以传递一个 python 列表(多维列表),如下图,使用 NumPy 去创建一个矩阵来表示他们:
np.array([[1,2],[3,4]])
还可以使用上面提到的方法( ones(), zeros(), 和 random.random() )只要提供一个元组来描述矩阵的维度信息,如下图:

矩阵运算
如果两个矩阵的行列数相同,我们可以使用运算符(+ - * /)对矩阵进行运算。NumPy 也是基于位置来进行操作:

这些运算符也可以在不同的行列数的矩阵上使用只要不同维度的矩阵是一个一维矩阵(例如,只有一行或一列),在这种形式上, NumPy 使用了 broadcast 规则来进行计算:

点积(Dot Product)
和前面的算术运算的一个关键区别是在对矩阵进行这类乘法(传统意义的矩阵相乘(译者注))时使用点积操作时,NumPy 为矩阵提供了一个 dot() 方法,可以计算出矩阵的点积:

我已经在图片的底部加入了矩阵的维度信息,强调了不同维度的矩阵,在点乘时相邻的维度必须相同(就是 1×3 的矩阵和 3×2的矩阵相乘,前者的列维度和后者的行维度相同(译者注))。你可以想象是进行了如下的操作:

矩阵索引
当我们使用矩阵的时候索引和切片功能将更加有用:

矩阵聚合
与向量(数组)相同,可以对矩阵进行类似的聚合操作:

而且不仅可以对矩阵中的所有值进行聚合,还能对行或列进行单独的聚合操作,使用 axis 参数进行指定(axis是轴的意思):

置换和变形
当处理矩阵时一个共用功能就是矩阵的变换。比如当需要计算两个矩阵的点积的时候可能需要对齐矩阵相邻的维度(使矩阵能够进行点积运算)。NumPy 的数组有一个很方便的属性 T 可以获取矩阵的转置:
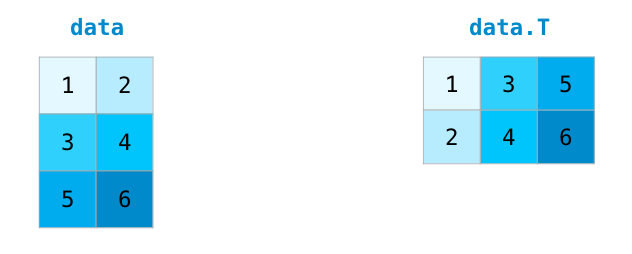
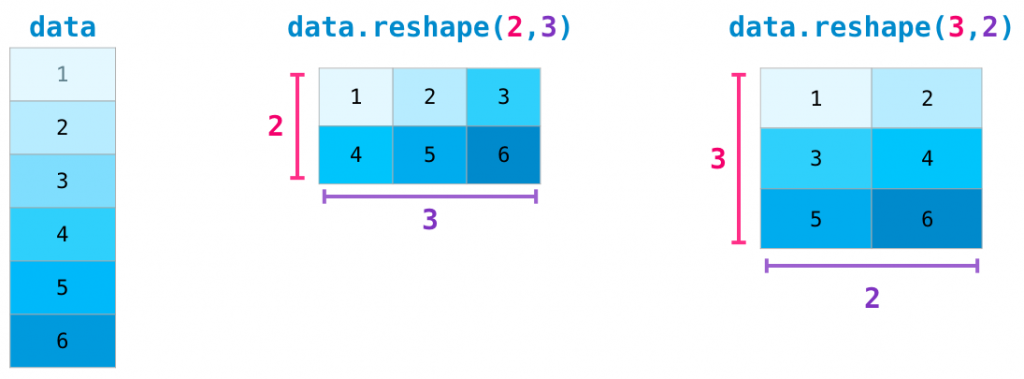
在更高级的场合,你可能发现需要变换矩阵的维度。这在机器学习中时经常常见的,比如当一个特定的模型需要一个一个特定维度的矩阵,而你的数据集的输入数据维度不一样的时候。NumPy 的 reshape() 函数就变得有用了。你只需指定你需要的新的矩阵的维度即可。你还可以通过将维度指定为 -1,NumPy 可以依据矩阵推断出正确的维度:
更高维度
在更高的维度,前面提及的,NumPy 都可以做到。其中一个主要原因就是被称为 ndarray(N-Dimensional Array)的数据结构。

在大部分场合,处理一个新的维度只需要在 NumPy 的函数上参数上增加一个维度:

注意:需要记住的是,当你打印一个3维的 NumPy 数组时,文本的输出和这里展示的不一样。NumPy 对多维数组的打印顺序是最后一个轴是最快打印的,而第一个是最后的。比如, np.ones((4, 3, 2)) 将会打印如下:
array([[[1., 1.],
[1., 1.],
[1., 1.]],
[[1., 1.],
[1., 1.],
[1., 1.]],
[[1., 1.],
[1., 1.],
[1., 1.]],
[[1., 1.],
[1., 1.],
[1., 1.]]])实际使用
现在是获取成果的时候了,下面是一些 NumPy 将会帮助你的一些例子。
公式
实现在矩阵和向量上的数学公式是NumPy的一个关键用处,这也是为什么 NumPy 是python 科学计算领域的宠儿。例如, 均方误差公式是解决回归问题的有监督机器学习模型的一个关键。

用 NumPy 来实现是一件轻而易举的事:

优雅之处在于 numpy 不关心 predictions 和 labels 的容量是 1 还是几百个值(只要它们有同样的容量)。我们可以通过如下四个步骤来对这行代码进行一个序列走读:

predictions 和 labels 向量都有3个值,也就是说 n = 3, 计算完减法后,我们得到如下的公式:

然后对这个向量求平方操作:

现在,我们对三个数进行求和:

error 中的值就是模型预测的质量
数据展示
考虑到所有可能需要处理和构建模型的数据类型(电子表格,图像,音频等)。很多是很适合用一个n维数组进行表示的。
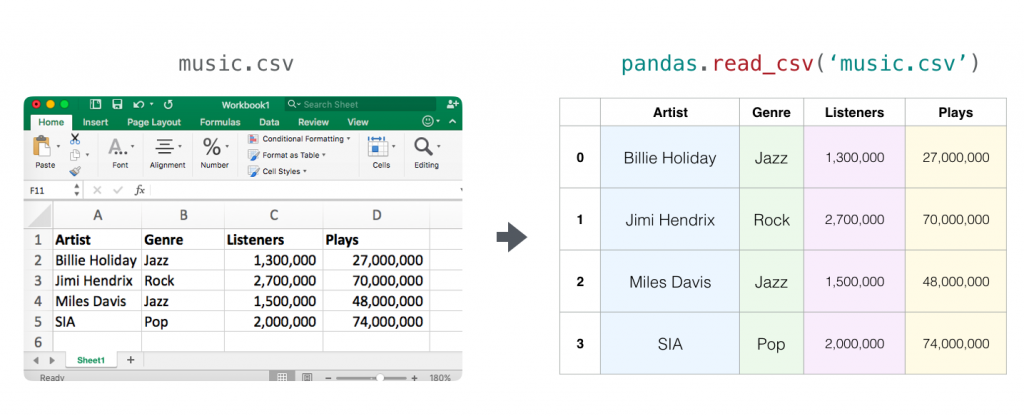
电子表格
- 电子表格是一个二维矩阵,每一个 sheet 页都有它的变量。python 中最流行的一个框架是
pandas dataframe,这也是一个使用 NumPy 构建的一个软件包。
音频和时间序列数据
- 一个音频文件是一个以为数组的样本。 每个样本都是一个数字,代表一小块音频信号。 cd质量的音频每秒可能有44,100个样本,每个样本是-32767到32768之间的整数。 这意味着如果您有一个10秒的cd质量的WAVE文件,您可以将它装入一个长度为10 * 44,100 = 441,000的NumPy数组中。 如果想提取音频的第一秒,只需将该文件加载到一个NumPy数组
audio中,并使用audio[:44100]即可获取到。
下面是一个音频文件的一个切片:

时间序列的数据也是一样(比如, 随时间变化的股票价格 )
图像
- 一个图像就是一个像素矩阵,其维度就是高度 x 宽度。
- 如果图像是黑白照片,也就是一个灰度图,每个像素可以用一个数字代表(通常是在0(黑)和255(白)之间)。如果 想要裁切图像左上角10 x 10像素的部分,只需通过 NumPy 的
image[:10, :10]函数即可获取
- 如果图像是黑白照片,也就是一个灰度图,每个像素可以用一个数字代表(通常是在0(黑)和255(白)之间)。如果 想要裁切图像左上角10 x 10像素的部分,只需通过 NumPy 的
下面是一个图片文件的切片:

- 如果是一个彩色图像,那么每个像素可以用3个数字表示——一个代表红色,一个代表绿色,一个代表蓝色。这种情况下,我们需要一个3维素组(因为每个单元仅可以包含一个数字)。因此,一个彩色图像可以被一个 ndarray 维度表示:(高度 * 宽度 * 3):

语言
如果我们处理的是文本的话,情况可能有点不同。要用数值表示一段文本需要构建一个词汇表(模型需要知道的所有的唯一词)以及一个词嵌入(embedding)过程。 让我们看看用数字表示这个谚语的步骤:” Have the bards who preceded me left any theme unsung?”
模型需要先训练大量文本才能用数字表示这位诗人的诗句。我们可以让模型处理一个小数据集,并使用这个数据集来构建一个词汇表(71,290个单词):

这个句子可以被划分为一系列词(token)(基于通用规则):

然后我们用词汇表中单词的ID来替换它:

对于模型来说,这些ID并没有提供更多的信息。因此,在将这些词喂入模型之前,需要先将她们替换为对应的词嵌入向量(本例中使用50维度的 word2vec 词嵌入)

可以看出这个 NumPy 数组有 [词嵌入维度 * 序列长度] 的维数。在实践中可能有另外的情况,在此我用这种方式来表示。出于性能因素的考虑,深度学习模型倾向于保存批处理数据的第一个维度(因为如果并行地训练多个实例,模型可以训练得更快)。reshape() 在这里就发挥了用武之地。比如像 BERT 这样的模型,他的输入希望是这种[批处理大小, 序列长度, 词嵌入维度]([ batch_size, sequence_length, embedding_size ]) 形状的。

现在,这些就是一个模型可以处理并且使用的一个数值型卷积向量。我在上图中的其他行留了空白,但是他们实际是被填充用于训练(或者是预测)。
留言
非常好的一篇文章,翻译的也很好。从搜狐转载的一路找回你的原文,特意来感谢一下。
谢谢肯定~ 搜狐转载的链接能给一个吗
从百度里搜到的这个: https://www.sohu.com/a/325758681_505915 然后看到转发来源于这个号: https://www.sohu.com/a/324639049_308467
嗯嗯,谢谢!