机器学习/评分卡常用指标及计算

点击数：1611

1. 信息熵

信息熵 (information entropy) 是度量样本集合纯度最常用的一种指标。假定当前样本集合 \(D\) 中第\(k\) 类样本所占的比例为 \(p_k(k=1,2,…|y|)\)，则 \(D\) 的信息熵定义为：

\(Ent(D) = -\sum_{k=1}^{|y|}p_klog_2p_k\)

\(Ent(D)\) 的值越小，则 \(D\) 的纯度越高

2. 信息增益

假定离散特征 F 有多个可能的取值：\(\{x_1, x_2, …, x_v\}\) ，则对特征的每个离散值，均可计算出取值为 \(x_v\) 的样本集合 \(D_v\) 的信息熵。再考虑到不同的特征值其包含的样本个数不同，给予离散特征值赋予权重 \(\frac{D_v}{D}\)，即样本数越多的特征值的影响越大。从而可以计算出用特征 F 对样本集 \(D\) 进行划分所获得的“信息增益” (infomation gain)

\(Gain(D, F) = Ent(D) – \sum_{v=1}^{v}\frac{|D_v|}{|D|}Ent(D_v)\)

• 例子：

如下是截取自 德国信用卡数据集 (adult_income) 的部分数据，将income标记为 0/1

其他特征	workclass	income	label
…	Private	<=50K	1
…	Private	<=50K	1
…	Private	>50K	0
…	?	<=50K	1
…	Private	<=50K	1
…	?	>50K	0
…	Self-emp-not-inc	<=50K	1
…	Private	<=50K	1
…	Private	>50K	0
…	?	<=50K	1
…	Self-emp-not-inc	>50K	0
…	Self-emp-not-inc	<=50K	1

本数据集中，类别数为 2 , 其中正例样本占比: \(\frac{8}{12}\), 负例样本占比: \(\frac{4}{12}\). 则初始时包含所有样本，则信息熵为：

\(Ent(D) = -\sum_{k=1}^{2}p_klog_2p_k = -(\frac{8}{12}*log_2\frac{8}{12} + \frac{4}{12}*log_2\frac{4}{12}) = 0.918\)

接下来选择 workclass 特征计算信息增益：

其中 Private 特征值的样本数为 \(6\)，其中标签为 0 的占比为\(\frac{2}{6}\) ，标签为 1 的占比为\(\frac{4}{6}\). ? 特征值的样本数为 \(3\)，其中标签为 0 的占比为 \(\frac{1}{3}\)，标签为 1 的占比为 \(\frac{2}{3}\). Self-emp-not-inc 特征值的样本数为 \(3\)，其中标签为 0 的占比为 \(\frac{1}{3}\)，标签为 1 的占比为 \(\frac{2}{3}\). 则，各个特征值对应的信息熵为：

\(Ent(Private) = -(\frac{2}{6}*log_2\frac{2}{6} + \frac{4}{6}*log_2\frac{4}{6}) = 0.918\)

\(Ent(?) = -(\frac{1}{3}*log_2\frac{1}{3} + \frac{2}{3}*log_2\frac{2}{3}) = 0.918\)

\(Ent(Self-emp-not-inc) = -(\frac{1}{3}*log_2\frac{1}{3} + \frac{2}{3}*log_2\frac{2}{3}) = 0.918\)

其信息增益为：\(Ent(D) – (\frac{6}{12} * Ent(Private) + \frac{3}{12} * Ent(?) + \frac{3}{12} * Ent(Self-emp-not-inc) ) = 0.0\)

• 用处：

特征分箱、决策树划分

3. WOE

WOE (Weight of Evidence) 描述的是变量与目标之间的关系。在变量与目标之间存在如下关系：

\(ln(\frac{P(Y=1|X_j)}{P(Y=0|X_j)}) = ln(\frac{P(Y=1)}{P(Y=0)}) + ln(\frac{f(X_j|Y=1)}{f(X_j|Y=0)})\) (由贝叶斯公式即可推出。)

上式等式右边第一项为常量，是样本的先验分布的对数几率，第二项即为WOE，即 \(ln(\frac{f(X_j|Y=1)}{f(X_j|Y=0)})\)，其中 \(f(X_i|Y)\) 为条件概率密度函数或离散型变量的概率分布

WOE 一般用于风控模型（逻辑回归/评分卡）建模的编码阶段，在此场景下，变量\(X_j\) 包含\(M\)个离散值，则该变量的 \(WOE=\sum_{i=1}^{M}ln\frac{bad_i/bad_{total}}{good_i/good_{total}}\)

3.1. WOE 编码在评分卡中的使用

3.1.1. 逻辑回归角度

• 说回线性回归 (Linear regression)

给定数据集 \(D = {(x_1, y_1), (x_2, y_2), …, (x_m, y_m)}\) “线性回归” 试图学得一个线性模型尽可能准确地预测出目标 \(y\)，即：

\(f(x_i) = w x_i + b\)，使得 \(f(x_i) \cong y_i\)

• 对数线性回归 (Log-linear regression)

可否令模型预测值逼近 \(y\) 的衍生物呢？譬如，假设 \(y\) 不是在常数尺度上变化，而是在指数尺度上变化，即：

\(ln y = w x_i + b\)

这就是“对数线性回归”，它实际上是在试图让 \(e^{w x_i + b}\) 逼近 \(y\). 虽然形式上仍然是线性回归，但实质上已经是在求取输入空间到输出空间的非线性函数映射，如下图所示：

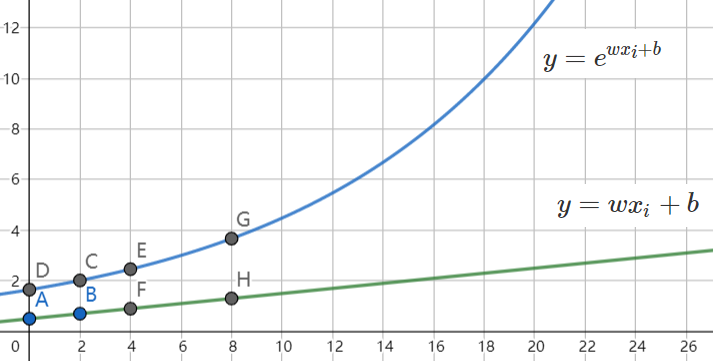
• 广义线性模型 (Generalized linear model)

更一般地，考虑单调可微函数 \(g(\cdot)\), 令：\(y = g^{-1}(wx_i + b)\), 这样得到的模型称为“广义线性模型”，其中的函数 \(g(\cdot)\) 称为“联系函数” (link function)。显然，对数线性回归是广义线性模型在 \(g(\cdot) = ln(\cdot)\) 时的特例。

• 对数几率回归 (Logistic regression / logit regression)

上述模型的输出均是实数，若要应用于分类任务该如何？参考对数线性回归，只需找一个单调可微函数将分类任务的\(y\) 与线性回归的预测值联系起来。

考虑二分类任务，其输出标记 \(y \in \{0, 1\}\)，于是，我们需要将线性回归的输出实值 \(z\) 转换为 \(0/1\) 的值。对数几率函数(Logistic function) 正是这样一个常用函数：

\(y = \frac{1}{1+e^{-z}}\)

它将\(z\) 值转化为一个在0和1之间的值。代入广义线性回归模型中：

\(y = \frac{1}{1+e^{-(wx_i + b)}}\)

视 \(y\) 为输出标记为正例的概率，则 \(1-y\) 是其反例的概率值，二者的比值：\(\frac{y}{1-y}\) 称为 “几率” (odds)，反映了样本 \(x\) 作为正例的相对可能性。对几率取对数则得到了对数几率 (log odds，亦称 logit)：

\(ln (\frac{y}{1-y}) = wx_i + b\)

从上式可以看出，这实际上是在用线性回归模型的结果去逼近真实值的对数几率，因此，对应的模型称为“对数几率回归” (logistic regression, 亦称 logit regression). 虽然名字仍然是“回归”，但实际上却是一种分类学习方法。

推广到多元的情形下，假设数据集 \(D\) 由 \(d\) 个特征组成，此时“多元线性回归”可表示为：

\(f(x) = \overrightarrow{w}^{T}\overrightarrow{x} + \overrightarrow{b}\)

3.1.2. 朴素贝叶斯角度

\(ln(\frac{P(Y=1|x_1,x_2,…,x_p)}{P(Y=0|x_1,x_2,…,x_m)}) = ln(\frac{P(Y=1) * P(x_1,x_2,…,x_m|Y=1)}{P(Y=0) * P(x_1,x_2,…,x_m|Y=0)}) = ln(\frac{P(Y=1)}{P(Y=0)}) + \sum_{j=1}^m ln(\frac{f(x_j|Y=1)}{f(x_j|Y=0)})\)

上式表明“对数几率等于先验对数几率与各特征的WOE值之和”。朴素贝叶斯假设各特征\(x_j\) 之间相互独立，这个假设过于严格。为此，在各个特征前加入系数 \(w_i\)：

\(ln(\frac{P(Y=1|x_1,x_2,…,x_p)}{P(Y=0|x_1,x_2,…,x_m)}) = ln(\frac{P(Y=1)}{P(Y=0)}) + \sum_{j=1}^m w_j * ln(\frac{f(x_j|Y=1)}{f(x_j|Y=0)})\)

当然这并不能完全拟合变量间的相关性。

3.1.3. 评分卡

想想我们如何构建一个方法去评估一个人的信用呢？我们可能会从多个角度去考虑：年龄、教育程度、工作性质等。然后根据每个维度的信息“综合考虑” (1)，同时不希望每个特征微小的变化不至于对分数产生很大的影响 (2)；并且希望得到的分数变化能定性地衡量其违约的概率 (3)。

根据条件 (1) 我们给每个维度的信息一个权重，并求和/求积，从简单考虑，线性回归即可根据各维度地分数组合为一个分数值，即 \(S = \overrightarrow{w}^{T}\overrightarrow{x} + \overrightarrow{b} \Rightarrow S = A * ln(\frac{p}{1-p}) + B\)；

根据条件 (2)，可以对每个维度进行分箱处理；

根据条件 (3)，可以假定一个变化的刻度，由于上一步用到了对数几率，则可假设当其可能违约的概率相比不违约的比值增加2倍时，其分数增加 \(PDO\) (Point to double the odds)：

\(S + PDO = A * ln(\frac{2p}{1-p}) + B\)

由此解出 \(A\) 和 \(B\) 的值，得到逻辑回归模型到评分卡的转换:

\(S = A * ln(\frac{p}{1-p}) + B = A*(\sum_j^m(w_j * WOE_j)) + B\)

4. IV

IV值一般用于二分类中的变量筛选，用IV来衡量变量对好坏样本的区分能力。其公式为：

\(IV = \sum_i^m (\frac{Bad_i}{Bad_{total}} – \frac{Good_i}{Good_{total}}) * woe_i\)

然而，为什么IV要如此定义，WOE不也能代表变量的预测能力么？

在介绍WOE后，通过其公式可以看到，变量 \(x_j\) 的每个woe值与对数几率正相关，即woe越大，其概率值 \(p(y=1|x=x_{jm})\) 越大(\(m\) 代表离散变量 \(x_j\) 的每个可能取值)。那么如何衡量整个变量 \(x_j\) 的预测能力（重要性）呢？用变量的 \(WOE=\sum_{i=1}^mwoe_i\)是否可行？

从WOE的公式上很容易看出，其值有正有负，则相加之后无法对变量的预测值进行比较。这也启发我们需要找到一个像度量两点之间的距离类似的概念，能度量变量对好坏样本的区分度。

KL散度 (Kullback-Leibler divergence)，也称为相对熵 (relative entropy) ，是两个概率分布间差异的非对称性度量。在离散型变量下，其公式为：

\(KL(P||Q)=\sum_{i=1}^mP(x_i)ln\frac{P(x_i)}{Q(x_i)}\), 其中 \(Q(x)\) 是近似分布，\(P(x)\) 是我们想要用 \(Q(x)\) 匹配的真实分布。

如果我们把 \(P(x)\) 看作坏样本在变量 \(x_j\) 上的分布，把 \(Q(x)\) 看作是好样本在变量 \(x_j\) 上的分布，通过KL散度，即可度量在变量 \(x_j\) 上的好坏样本的分布差异，也即变量区分好坏样本的能力。

然而KL散度是一个非对称性的度量，即 \(KL(P||Q) \ \neq \ KL(Q||P)\)。作为一个度量，我们希望分布 \(Q\) 到分布 \(P\) 的“距离”和分布 \(P\) 到分布 \(Q\) 的“距离”应该一样。可以证明KL散度：

在固定概率分布 \(P(x)\)（或 \(Q(x)\)）的情况下，对于任意的概率分布 \(Q(x)\)（或\( P(x)\)），都有 \(KL(P(x)||Q(x))≥0\)，而且只有当 \(P(x)=Q(x)\) 时才等于零。

由于KL的非负性，那么 \(KL(P||Q) + KL(Q||P)\) 不就是一种具有对称性的分布 \(P\) 到分布 \(Q\) 的“距离”度量了嘛！我们试着写出度量变量 \(x_j\) 好坏样本差异的公式：

\(\sum_i^mP(x_{ji}|y=1)*ln\frac{P(x_{ji}|y=1)}{P(x_{ji}|y=0)} + \sum_i^mP(x_{ji}|y=0)*ln\frac{P(x_{ji}|y=0)}{P(x_{ji}|y=1)}\)

整理一下，得到：

\(\sum_i^m(P(x_{ji}|y=1) – P(x_{ji}|y=0))*ln\frac{P(x_{ji}|y=1)}{P(x_{ji}|y=0)} = \sum_i^m(P(x_{ji}|y=1) – P(x_{ji}|y=0)) * woe_i\)

上述既是IV的表达式。

5. lift

lift 值代表使用模型时的效果较不使用模型时的效果的提升值。则涉及到两个值，“使用模型时的效果”——T，以及 “不使用模型时的效果”——R.

\(lift = \frac{T}{R}\)

在二分类场景中，将模型对训练集/验证集样本 \(D\) 预测的概率值按从大到小的顺序排列：

选取数据的 \(N\) 个切分点，在第i个切分点 \(\frac{i}{N}\) 处，计算模型预测对的累计正例值 \(T=\sum_{j=0}^iTi\)，即得到“使用模型时的效果”；再除以“不使用模型时的效果”，即先验正例值 \(R=len(D| y=1) * \frac{i}{N}\) 即可得到lift曲线：

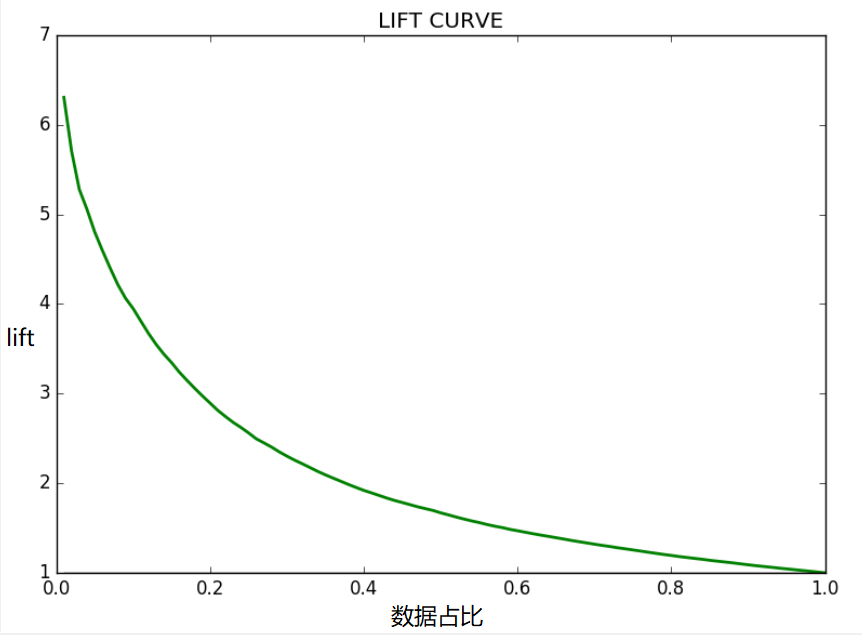
在评分卡应用场景中，常常使用评分分段代替概率，则可使用分段累计坏样本除以总的坏样本即可得到各区间lift值，如下表：

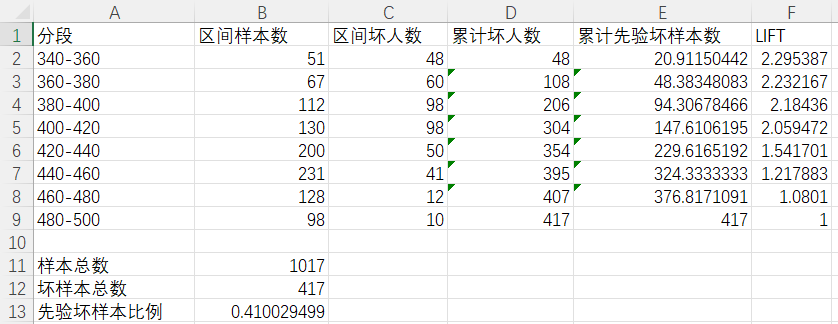
明天再更。。。

参考：

周志华. 机器学习[M]. 2016年1月第1版. 清华大学出版社, 2018.

KIM LARSEN. Data Exploration with Weight of Evidence and Information Value in R[EB/OL]. [2022-06-25]. https://multithreaded.stitchfix.com/blog/2015/08/13/weight-of-evidence/.

https://www.geeksforgeeks.org/understanding-gain-chart-and-lift-chart/

Kullback, S. and Leibler, R.A., 1951. On information and sufficiency. The annals of mathematical statistics, 22(1), pp.79-86.